Angle between two lines

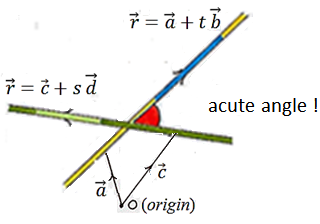
Consider two vectors:

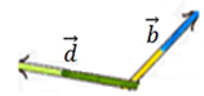
then the acute angle θ between two straight lines is given by:

Where b and d can be considered as the direction vectors of the two lines as shown above. The lines do not have to be intersecting – the angle is the angle between them if one was moved along so they do intersect.

In case the lines L₁ and L₂ do not pass through the origin, we may consider that lines L₁’ and L₂’are parallel to L₁ and L₂ respectively and pass them throughthe origin so that these lines have the same equation with different free vector.

Suppose direction cosines of two lines L₁ and L₂ are given: (l₁, m₁, n₁) and (l₂, m₂, n₂) then we can find the acute angle in the following manner:

$\cos \theta =\vert l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}\vert $

Note that, two lines containing direction ration a₁, b₁, c₁ and a₂, b₂, c₂ are considered as:

1. Perpendicular where θ =90°
   
   Therefore:$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}=0$
2. Parallel where θ =0°
   $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}
   $

Therefore:

Now, let us consider the angle between two lines when their equations are given in the question. If θ is assumed as an acuteangle then the angle between the lines can be written as:

$\overrightarrow{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}$

$\overrightarrow{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}$

Therefore, in the cartesian form we can write: $\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}$

Also: $\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}$

Therefore, to find the acute angle using direction ratio we can write:

$\cos \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $

Example: Find the acute angle between the lines with vector equations:

r = (2i + j + k) + t(3i – 8j – k)

and r = (7i + 4j + k) + s(2i + 2j + 3k)

Solution:

$a=(\begin{matrix}
3 & \\
-8 & \\
-1 & \\
\end{matrix}
);b=(\begin{matrix}
2 & \\
2 & \\
3 & \\
\end{matrix}
)$

Calculate the dot product of a and b

$a.b=(\begin{matrix}
3 & \\
-8 & \\
-1 & \\
\end{matrix}
).(\begin{matrix}
2 & \\
2 & \\
3 & \\
\end{matrix}
)$

$a.b=(3\times 2)+(-8\times 2)+(-1\times 3)$

$a.b=-13$

Now calculate the magnitude of a and b:

$\vert a\vert =\sqrt{3^{2}+(-8)^{2}+(-1)^{2}}$

$a|=\sqrt{74}$

$\vert b\vert =\sqrt{2^{2}+2^{2}+3^{2}}$

$|b|=\sqrt{17}$

Substitute the values above to find the angle:

$\cos \theta =\vert  \frac{a.b}{\vert a\vert |b|} \vert $

$cos\theta =\vert  \frac{-13}{\sqrt{74}\sqrt{17}} \vert $

$cos\theta =\vert  -0.3665\ldots \vert $

Since the answer is negative, we need to ‘make it positive’ by multiplying by -1

$cos\theta =0.3665$

$\theta =68.5deg$

Example: Consider the pair of lines given below, find the angle between them.
$\frac{x-3}{3}=\frac{y-1}{5}=\frac{z+3}{4}$

$\frac{x+1}{1}=\frac{y-4}{1}=\frac{z-5}{2}$

Solution: in the cartesian form recall that: $\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}$

The direction ratios of the first line can be seen from the cartesian equation are 3, 5, 4 and for the second line are 1, 1, 2. If θ is the angle between them, they can be written as:

$\cos \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $

$\cos \theta =\vert \frac{3\cdot 1+5\cdot 1+4\cdot 2}{\sqrt{3^{2}+5^{2}+4^{2}}\cdot \sqrt{1+1+2^{2}}}\vert =\frac{8\sqrt{3}}{15}$

Hence we can find the required acute angle by taking $\cos ^{-1}\frac{8\sqrt{3}}{15}$