The area between any of the two of lines, circles/parabolas/ellipses (the region should be clearly identifiable)
Find the area enclosed by two sections: a line at y = x – 1 and the parabola y2 = 2x + 6.
By solving the two equations, we find that the points of intersection are (-1, -2) and (5, 4).
We use the equation of the parabola and solve for x.
From the figure as seen below, we deduce that the left and right boundary curves are:
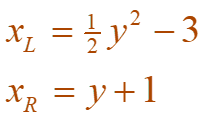
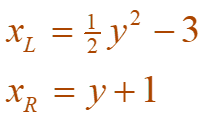
We must integrate between the appropriate y-values as seen from the graph above, y =-2 and y =4.
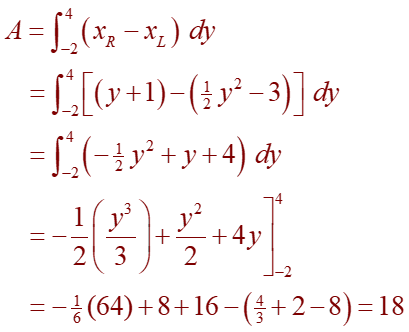
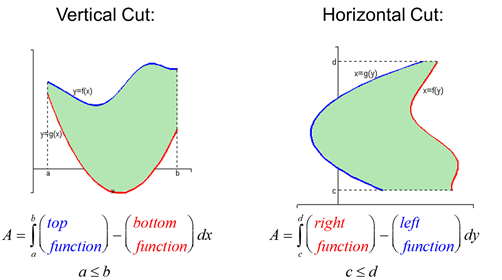
To find the area between the curves y = f(x) and y = g(x), where f(x) ≥ g(x) for some values of x but g(x) ≥ f(x) for other values of x. We then split the given region S into several regions S1, S2, . . . with areas A1, A2, . . .Then, we define the area of the region S to be the sum of the areas of the smaller regions S1, S2, . . . , that is, A = A1 + A2 +. . .
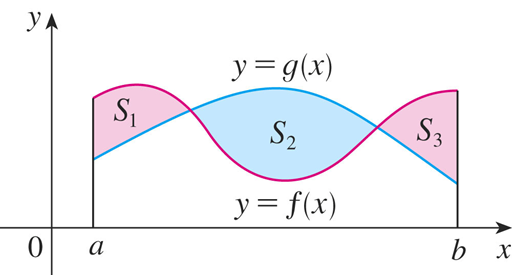
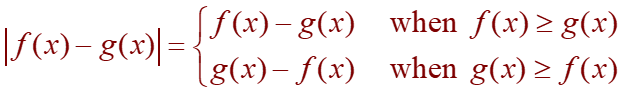
The area between the curves y = f(x) and y = g(x) and between the closed interval of x= a and x = b is:
![]()
Example: Find the area of the region bounded by the curves y = sin x, y = cos x, x =0, and x = π/2.
The points of intersection occur when sin x = cos x, that is, when x = π / 4 (since 0 ≤ x ≤ π / 2).
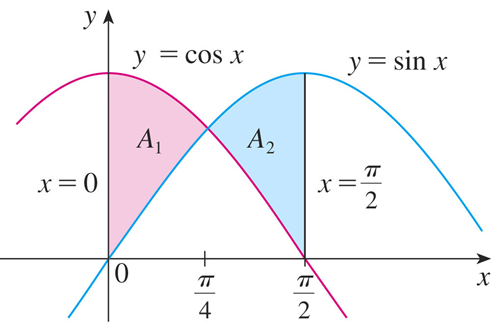
Observe that cos x ≥ sin x when 0 ≤ x ≤ π/ 4 but sin x ≥ cos x when π/ 4 ≤ x ≤ π/ 2.
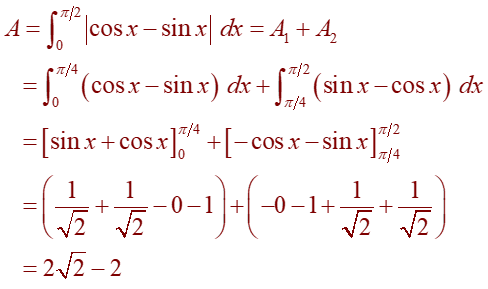
In general:
Find the area between an ellipse and the coordinates x = 0 and the ordinates x = 0
and x = ae, also b2 = a2 (1 – e2) and e < 1.
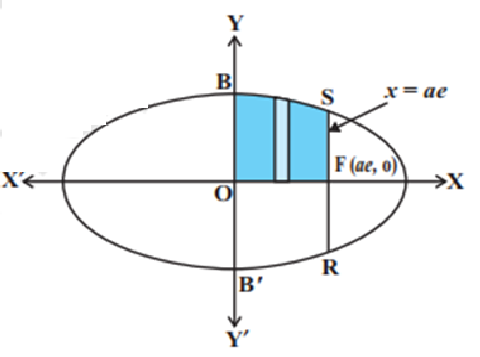
The required area of the region BOB′RFSB is enclosed by the ellipse and the lines x = 0 and x = ae. Note that the area of the region BOB′RFSB
$=2\int_{0}^{ae}{y dx}=\frac{2b}{a}\int_{0}^{ae}{\sqrt{a^{2}-x^{2}}dx}$
$=\frac{2b}{a}\lbrack \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin ^{-1}\frac{x}{a}\rbrack _{0}^{ae}$
$=\frac{2b}{2a}\lbrack ae\sqrt{a^{2}-a^{2}e^{2}}+a^{2}\sin ^{-1}e\rbrack $
$=ab\lbrack e\sqrt{1-e^{2}}+\sin ^{-1}e\rbrack $
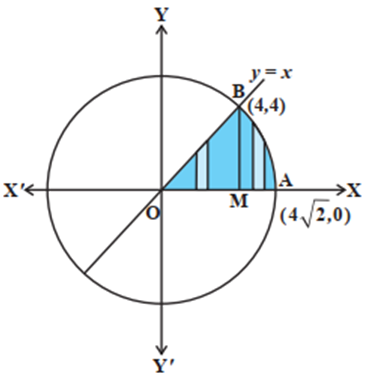
Example: Find the area of the region in the 1st quadrant between by the line y = x, a circle x2+ y2 = 32 and the x-axis.
There are two equations: y = x and x2+ y2 = 32
Solving (1) and (2), we find that the line and the circle meet at B(4, 4) in the 1stquadrant. Draw perpendicularBM to the x-axis. Therefore, the required area = area of the region OBMO + area of the region BMAB.
Now, the area of the region OBMO
$=\int_{0}^{4}{ydx}=\int_{0}^{4}{x dx=\frac{1}{2}\lbrack x^{2}\rbrack _{0}^{4}=8}$
The area of the region BMAB:
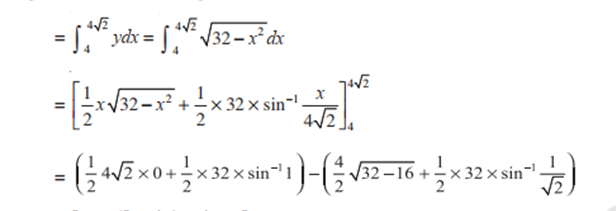
= 8π – (8 + 4π) = 4π -8
Adding the two sections we get: 4π