Cartesian and vector equation of a plane

A plane can be completely illustrated by denoting two intersecting lines which can be translated into a fixed point A and two nonparallel direction vectors. The position vector $\overrightarrow{r}$ of any general point P on the plane passing through point A and having direction vectors  $\overrightarrow{b}$ and $\overrightarrow{c}$ is given by the equation

Vector equation of a plane

$\overrightarrow{r}=\overrightarrow{a}+\lambda  \overrightarrow{b}+µ\overrightarrow{c}                \lambda, µ∈R                        (\overrightarrow{AP}=\lambda  \overrightarrow{b}+µ\overrightarrow{c})$

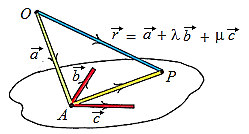
Parametric equation of a plane: λ , μ are called a parameters λ,μ ∈ R
$ (\begin{matrix}
x & \\
y & \\
z & \\
\end{matrix}
)=(\begin{matrix}
a_{1} & \\
a_{2} & \\
a_{3} & \\
\end{matrix}
)+\lambda (\begin{matrix}
b_{1} & \\
b_{2} & \\
b_{3} & \\
\end{matrix}
)+\mu (\begin{matrix}
c_{1} & \\
c_{2} & \\
c_{3} & \\
\end{matrix}
)  =>    \begin{matrix}
x=a_{1}+\lambda b_{1}+\mu c_{1} & \\
y=a_{2}+\lambda b_{2}+\mu c_{2} & \\
z=a_{3}+\lambda b_{3}+\mu c_{3} & \\
\end{matrix}
$

If N is considered to be normal to a given plane, then all other normals to that plane are considered parallel to N which are resultantly scalar multiples of N., In particular,we can say that there are two normals of length 1:

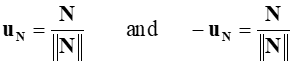
Normal/Scalar product form of vector equation of a plane

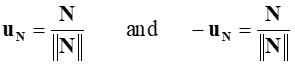
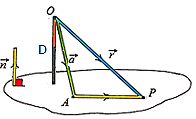
Consider a vector n passing through a point A. Only one plane through A can be is perpendicular to the vector. Now consider R being any point on the plane other than A as shown above. Then we can say that

$\overrightarrow{n}.\overrightarrow{AR}=0$

$\overrightarrow{n}.\overrightarrow{(r}-\overrightarrow{a})=0$

$\overrightarrow{n}.\overrightarrow{r}=  \overrightarrow{n}.(\overrightarrow{a}+\lambda \overrightarrow{b}+µ\overrightarrow{c})$\textit{⇒}$
     \overrightarrow{r}.\overrightarrow{n}=\overrightarrow{a}.\overrightarrow{n}   or  \overrightarrow{n}.(\overrightarrow{r}-\overrightarrow{a})= 0
$

Cartesian equation of a plane

$\overrightarrow{r}.\overrightarrow{n}=\overrightarrow{a}.\overrightarrow{n}    ⤇     n_{1}x+n_{2}y+n_{3}z=n_{1}a_{1}+n_{2}a_{2}+n_{3}a_{3 }=d$

$n_{1}x+n_{2}y+n_{3}z=d$

$D=  \vert \overrightarrow{r}.{n}\vert =\vert \overrightarrow{a}.{n}\vert $

{=}$\frac{\vert \overrightarrow{a}.\overrightarrow{n}\vert }{\sqrt{n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}=\frac{\vert n_{1}a_{1}+n_{2}a_{2}+n_{3}a_{3 }\vert }{\sqrt{n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}$

Therefore, the Cartesian form is

where n₁, n₂ and n₃ are the components of n and where n is called the normal vector.

Example: Find the equation of the plane passing through the three points P₁(1,-1,4), P₂(2,7,-1), and P₃(5,0,-1).

$\overrightarrow{b}=\overrightarrow{P_{1}P_{2}}=  (\begin{matrix}
1 & \\
8 & \\
-5 & \\
\end{matrix})$

$\overrightarrow{c}=  \overrightarrow{P_{1}P_{3}} =  (\begin{matrix}
4 & \\
1 & \\
-5 & \\
\end{matrix}
)$

$P_{1}=(\begin{matrix}
1 & \\
-1 & \\
4 & \\
\end{matrix}
)$

In vector form:

$ \overrightarrow{r}=(\begin{matrix}
1 & \\
-1 & \\
4 & \\
\end{matrix}
) +\lambda  (\begin{matrix}
1 & \\
8 & \\
-5 & \\
\end{matrix}
)+µ(\begin{matrix}
4 & \\
1 & \\
-5 & \\
\end{matrix}
)$

$\overrightarrow{n}=\vert \begin{matrix}
{i} & {j} & {k} & \\
1 & 8 & -5 & \\
4 & 1 & -5 & \\
\end{matrix}
\vert =(\begin{matrix}
-35 & \\
-15 & \\
-31 & \\
\end{matrix}
)$

Any non-zero scalar multiples of $\overrightarrow{n}$ is also a normal vector of the plane. Therefore, Multiply by -1.

$\overrightarrow{n}=(\begin{matrix}
35 & \\
15 & \\
31 & \\
\end{matrix}
)$

$(\begin{matrix}
35 & \\
15 & \\
31 & \\
\end{matrix}
).(\begin{matrix}
1 & \\
-1 & \\
4 & \\
\end{matrix}
)=144$

$Cartesian form:$

$35x+15y+31z=144$

Example: Find the equation of the plane with normal vector $
(\begin{matrix}
1 & \\
3 & \\
5 & \\
\end{matrix}
)$containing the point (-2, 3, 4).

$(\begin{matrix}
1 & \\
3 & \\
5 & \\
\end{matrix}
).(-2,3,4)=-2+9+20=27$

x+3y+5z=27

Example: Find the distance of the plane $
\overrightarrow{r}.(\begin{matrix}
3 & \\
2 & \\
-4 & \\
\end{matrix}
)$ = 8 from the origin, and the unit vector perpendicular to the plane.

$\vert (\begin{matrix}
3 & \\
2 & \\
-4 & \\
\end{matrix}
) \vert =\sqrt{29}$

$\frac{1}{\sqrt{29}}\lbrack  \overrightarrow{r}.(\begin{matrix}
3 & \\
2 & \\
-4 & \\
\end{matrix}
)\rbrack  = \frac{8}{\sqrt{29}}$

$D=  \frac{8}{\sqrt{29}}        {n}= \frac{1}{\sqrt{29}}(\begin{matrix}
3 & \\
2 & \\
-4 & \\
\end{matrix}
)$

Example: Find the Cartesian equation of the plane through the point A (1, 1, 1) perpendicular to the vector

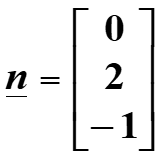
Solution:

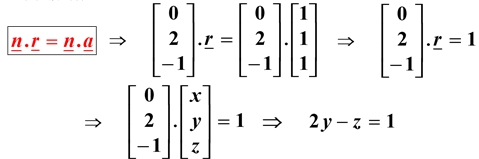
Example: Show that the following vector is perpendicular to the plane containing the points A(1, 0, 2), B(2, 3, -1) and C(2, 2, -1 ).

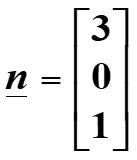
Solution:

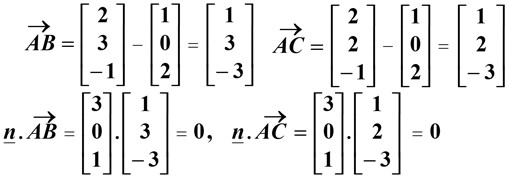
In conclusion, n is a vector that is perpendicular to 2 vectors in the plane so it is perpendicular to the plane.