1. A force is applied horizontally on a uniform rod of length L kept on a surface. Calculate the tension in the rod at a distance r from the end where the force is applied.
Let the mass of rod be M, and applied force is F.
Acceleration produced in the rod $a=F/M$
The free body diagram for the above problem is shown.
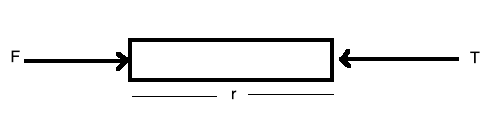
Using Newton’s second law,
$F-T=\frac{M}{L}r.a$
Or, $T=F-$$\frac{M}{L} r\frac{F}{M} $
Or, $T=F(1-r/L)$
2. A person weighs 300 N in a lift which is at rest. When the lift is accelerated, the tensile force is 650 N. Calculate the acceleration of the lift. Consider $g=10 m/s^{2}$.
Given, $w=300 N$, $T=650 N$, $g=10 m/s^{2}$
We get mass, $m=300/10=30 kg$
Initially, lift is at rest,hence acceleration $a=0$a = 0).
As the tensile force is greater than 300 N, so the lift accelerates
upward.
Therefore,
$T-mg=m a$
Or, $650-300=30\times a$
Or, $a=350/30=11.67 m/s^{2}$.
3. A mass of 5 kg is suspended by a rope of length 2 m from a ceiling. A horizontal force of 45 N is applied at the midpoint R of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium? Consider $g=10 m/s^{2}$.
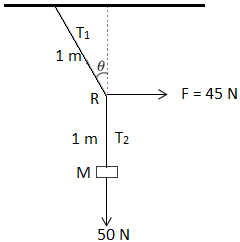
The free body diagram is shown.
As the mass is in equilibrium, the sum of all the external forces on the mass should be zero.
Therefore, $T_{2}=50N$
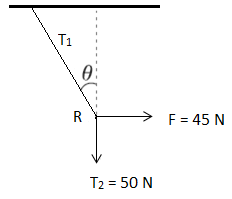
Next, we draw the free body diagram of the point R.
As the point R is also in equilibrium, the sum of all the forces at this point should be zero.
Then, $T_{1}cos \theta =45 N$ and $T_{1}sin \theta =50 N$
So, $tan \theta =50/40$
Or, $\theta =tan^{-1}(5/4)$= $48^{0}.$
4. A block of mass of 7 kg rests on a horizontal plane. The plane is gradually inclined at an angle $20^{0}$ such that the block just begins to slide. Calculate the coefficient of static friction.
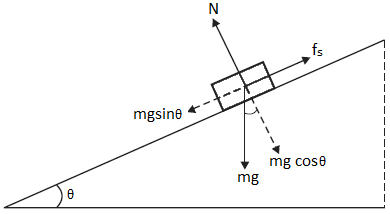
As the angle of inclination $\theta $ increases, frictional force $F_{s}$\textit{ }increases until at $\theta =\theta _{\max }$$F_{s}$ achieves its maximum value.
Then, $F_{s (max)}=\mu N$\ldots \ldots \ldots \ldots .. (1)
We get from the diagram, $mg sin\theta =F_{s}$ and $mg cos\theta =N$
Then from equation (1), we get,
$mg sin\theta _{\max }$=$\mu mg cos\theta _{\max }$
Or, $\tan \theta _{\max } =\mu $
Or, $\mu =tan 20^{0}=0.36$
5. A ball of mass $5kg$ and a block of mass $12kg$ are attached by a lightweight cord that passes over a frictionless pulley as shown. The block is on a frictionless surface of inclination angle 30$^{o}$. Find the magnitude of the acceleration of the two objects and the tension in the cord. Consider $g=10 /s^{2}$.
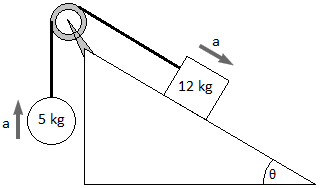
As the objects are connected by a cord, their accelerations have the same magnitude.
Free body diagrams are shown for the two objects.
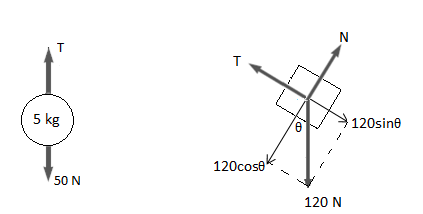
Normal force, $N=120 cos 30 = 60\sqrt{3}$= 104 N
Also, $120 sin 30-T=m a$
Or, $120 sin 30-T=12 a$
Or, $a=(60-T)/12$ \ldots \ldots \ldots \ldots \ldots \ldots \ldots (1)
Also, for the ball, $T-50=5 a$ (as both the objects have the same acceleration) \ldots \ldots \ldots \ldots (2)
From equations (1) and (2), we get,
$T-50=5$$(60-T)/12$
Or, $T=52.94 N$
Putting the value of T in equation (1), we get,
$a=(60-52.94)/12$
Or, $a=0.59 m/s^{2}$.
