According to the atomic model of Niel Bohar, the electrons which are having negative charge are revolving around the nucleus of an atom that is positively charged. This movement is in the circular orbit having the radius r. The revolving of electrons is in the closed path that constitutes the electric current. If the motion of electrons is in an anticlockwise direction, then there is a production of current in a clockwise direction.
The current I= e/T, and here T is representing a period of revolution of electrons. Here the orbital velocity is represented by V and the following situation can be stated.
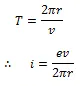
Due to the motion of electrons in orbits, an orbital magnetic moment will result.
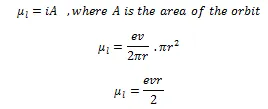
If the mass of electron is represented by m, then
![]()
Here mvr is angular momentum of an electron around the center of nucleus.
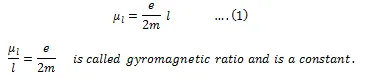
The value of this angular momentum is 8.8 × 1010 C kg-1. According to the hypothesis of Bohar, the angular momentum can only have a discrete set of values that are given by the below equation.
![]()
Here n is the natural number, and h is used to represent Plank’s constant and its value is 6.626 × 10-34 Js.
Here by the substitution of equation 2 from equation 1, the following condition can be stated.
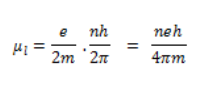
The minimum value associated with the magnetic moment can be represented by below equation.
![]()
This value of eh/4πm, is known as the Bohr magneton. By the substitution of values of m, h, and e, the calculated value of Bohar magneton is 9.27 × 10–24 Am2. In addition to magnetic momentum that is resulted due to orbital motion, the magnetic moment possessed by electrons is the vector sum of orbital magnetic moment and the spin magnetic moment. The ratio of magnetic dipole moment to the angular momentum of the revolving electron is known as the gyromagnetic ratio. The value of electron orbital factor is always equal to one, so by using quantum mechanical arguments the classical gyrometric ratio can be derived.
The example of hydrogen is most significant for this phenomenon. The atom of hydrogen interacts with external magnetic fields such as pull and push between the two bar magnets. If the magnetic moment is in antiparallel direction to the external magnetic field then the associated potential energy is large but if the magnetic moment is in a parallel direction, then this energy is usually small. An intrinsic property of electron is spin magnetic moment. Whereas, the orbital magnetic dipole moment is also associated with the with the revolving electron in the axis.
