The General solution of trigonometric equations of the type sin y = sin a, cos y = cos a and tan y = tan a
General Solution: The entire set of the values belonging to the unknown angle satisfies the equation. Also, it has all the specific solutions along with the principal solutions.
General Solutions of a Trigonometric Equation
From the below-given diagram, we can observe that sin(π -θ) = sin θ & cos ( -θ) = cos θ.
We use the above description for finding the solutions of a few trigonometric equations.
Now, Solve sin(x) = y for x.
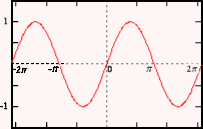
Case 1: When the condition is -1≤y≤ 1, i.e, y’s value is between
(-1 & 1), so, there’s the solution.
sin(x) = y is the set of all the possible solutions which is:
x = sin-1(y) + 2kπ & x = −sin-1(y) + (2k+1) π, Where “k” can be taken as any integer; i.e, solutions for x is having sin-1(y) in addition to all the even multiples of the value π, together with the minus sin-1(y) & all the odd multiples regarding π.
Case 2: When -1 > y or y > 1, i.e, y’s value is very much large or very much small for the possible solution.
There’re no solutions.
Solving Cos (x) = y for x.
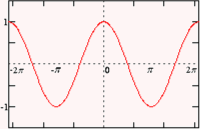
Case 1: -1≤y≤ 1
cos(x) = y is the set of all the solutions which is equal to
x = ± cos-1(y) + 2kπ,
Where “k” can be taken as any integer;
Case 2: When, -1 > y or y > 1
There exist no solutions.
Solving tan(x) = y for x.
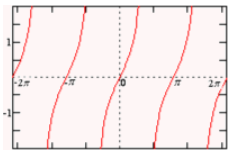
Tan(x) = y equation is the set of all solution to:
x = tan-1(y) + kπ,
Where the value of “k” can be taken as “any integer”
Example
Find the general solutions of √ 2 sinx = 1.
The equation is equivalent to Sinx = $\frac{1}{√2}$
Now, Sin ⁻¹ = $\frac{\pi }{4}$
Hence the general solution is
x = ±π/4 + 2kπ, where the value of k can be any integer.
Trigonometric Equations with their General solutions
| Trigonometrical Equation | General Solution |
| Sin θ = 0 | θ = nπ |
| Cos θ = 0 | θ = nπ + π/2 |
| Tan θ = 0 | θ = nπ |
| Sin θ = 1 | θ = 2nπ + π/2 |
| Cos θ = 1 | θ = 2nπ |
| Sin θ = a | θ = nπ ± (-1)ⁿa |
| Cos θ = a | θ = 2nπ ± a |
| Tan θ = a | θ = nπ ± a |
| Sin²θ = Sin²a | θ = nπ ± a |
| Cos²θ = Cos²a | θ = nπ ± a |
| Tan²θ= Tan²a | θ = nπ ± a |
| Sin θ = Sin a Cos θ = Cos a | θ = nπ ± a |
| Sin θ = Sin a Tan θ = Tan a | θ = nπ ± a |
| Tan θ = Tan a Cos θ = Cos a | θ = nπ ± a |
