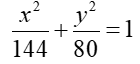Standard equation and properties of the ellipse

The equation of an ellipse with its centre at the origin has one of two forms:

Horizontal Ellipse

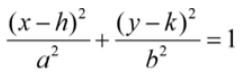
Foci:

Vertical Ellipse:

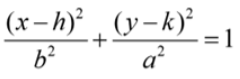
       Foci:

For a horizontal Major Axis and C(0,0): major axis = 2a and minor axis = 2b

For a Horizontal Major Axis and C(h,k):

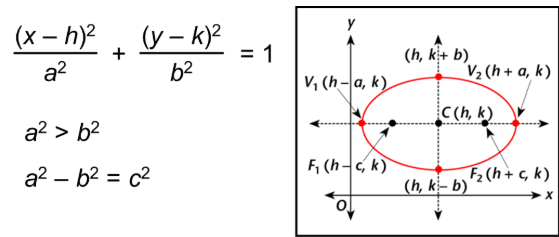
For a Vertical Major Axis and C(0,0), major axis = 2a and minor axis = 2b:

For a vertical Major Axis and C(h,k):

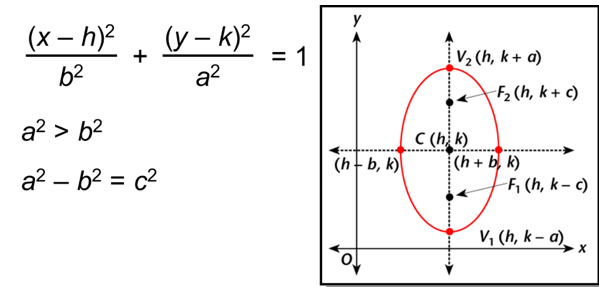
From the standard equations as explained above, we can make the following observations:

1. An ellipse is symmetric with respect to the major and minor axis. If (x, y) is a point on the ellipse, (-x, y), (x, -y) and (-x, -y) also exist on the ellipse.
2. The foci are present on the major axis which can be deduced by finding the intercepts on the axes of symmetry. This means that the major axis is along the x-axis when the coefficient x² has the bigger denominator. The major axis is along the y-axis when the coefficient of y² has the bigger denominator.

Steps for writing the equation of the ellipse in standard form:

1. Complete the square for both the x-terms and y-terms and move the constant to the other side of the equation
2. Divide all terms by the constant

Example 1:

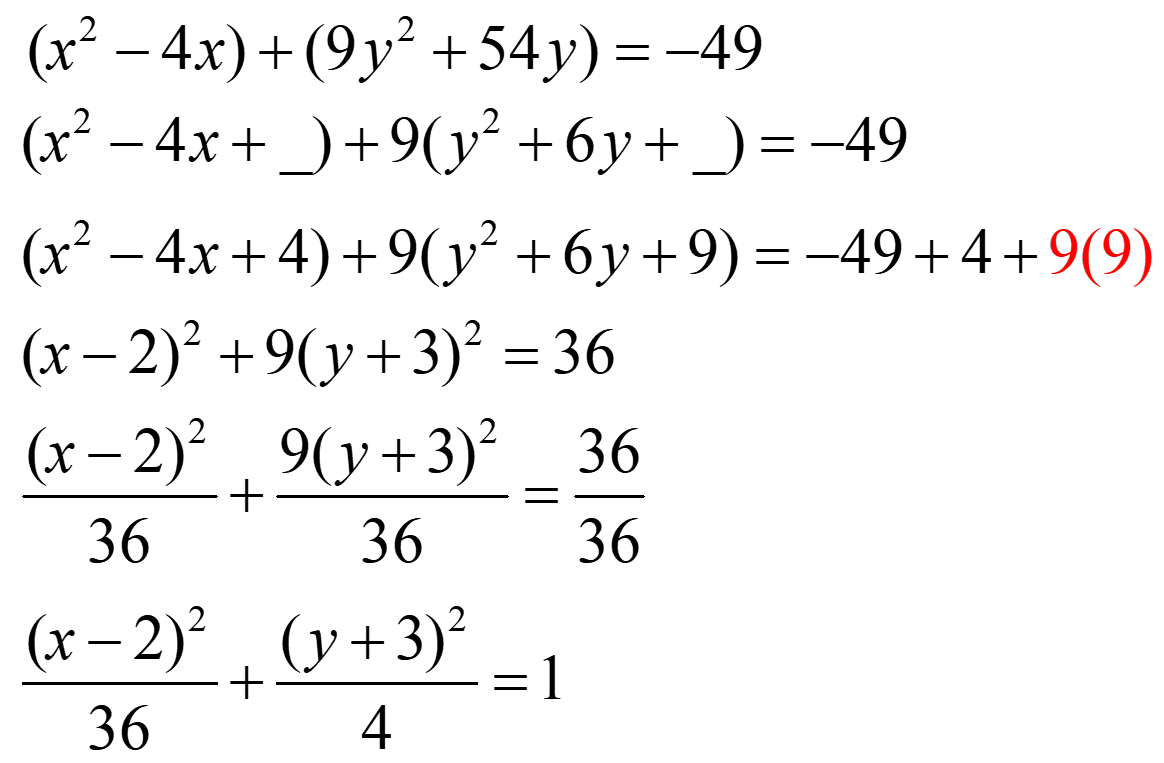
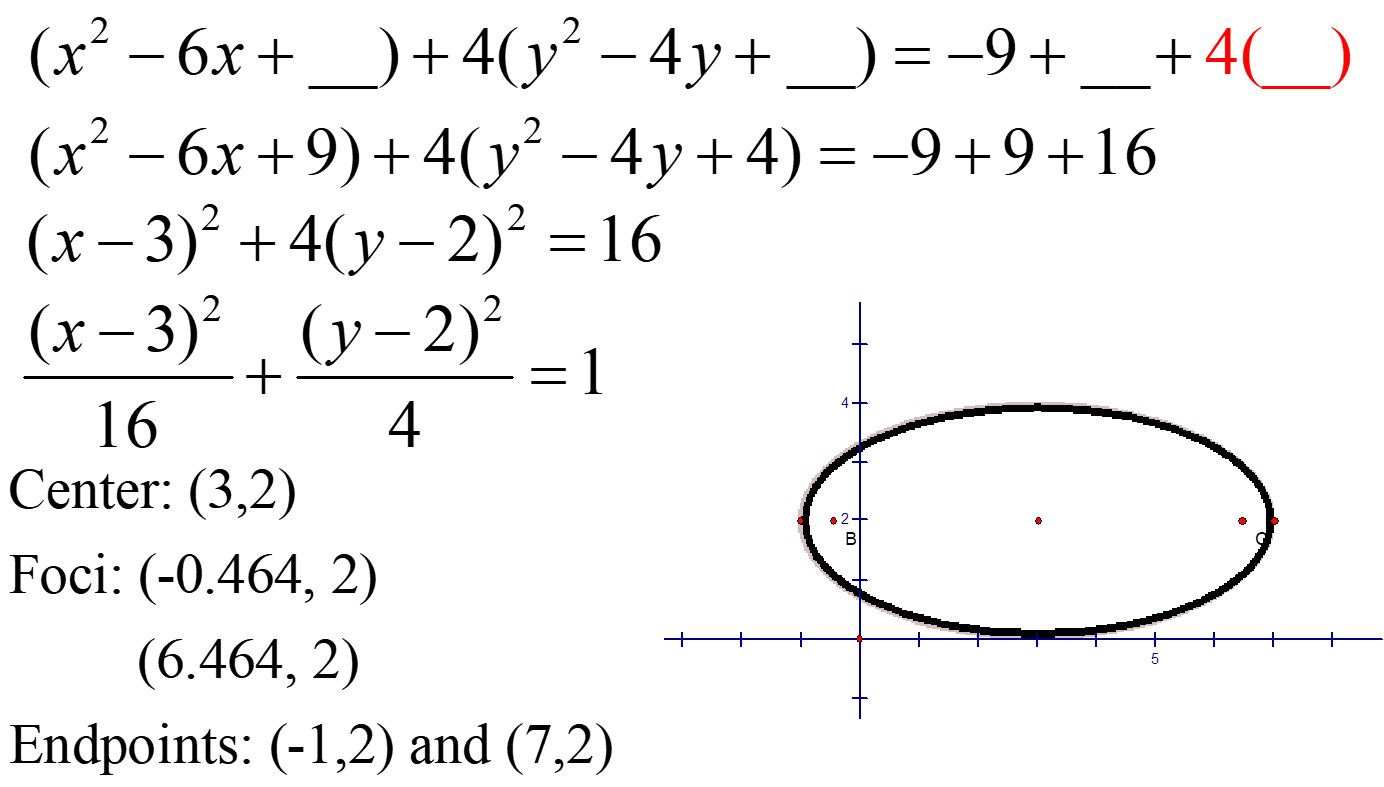
Steps for graphing the ellipse:

1. Put equation in standard form
2. Graph the centre (h, k)
3. Graph the foci (look at the equation to determine your direction)
4. Graph a units and –units from the centre to get the endpoints (horizontally if under x, vertically if under y)
5. Connect the endpoints

Example 2: Write the following equation in standard form, then graph it:

Example 3: Find the equation of the ellipse with foci at (8,0) and (-8,0) and a vertex at (12,0).

• First, place these points on axes. The F and F’ are the foci.
• Since the vertex is on the horizontal axis, the ellipse will be of the form:
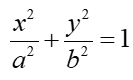
• The values of a and b need to be determined.
• Because the foci are at 8 and -8, c = 8. Also, the vertex is at (12,0), hence a = 12. Relating these values to the standard form for an ellipse whose centre is at the origin and whose major axis is horizontal, the equivalence c² = a² – b² applies. Solve for b² where
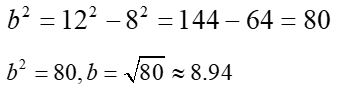
• The value of a is 12, and a² is 144.
• So the equation of the ellipse is: