Physical quantities are divided into two categories:
- Scalars quantities: They have only the magnitude. For example, mass, length, time, temperature etc. The scalars quantities can be added, subtracted, multiplied and divided just as the ordinary numbers.
- Vectors quantities: They have both magnitude and direction. for example velocity, force, electric field, torque etc.
A vector can be defined as a line segment having a specific direction and a specific length. The length is the magnitude of the vector and with an arrow indicating the direction. The direction is from the tail of the vector to its head.
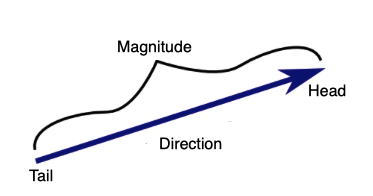
Figure:5.a
A vector is denoted by the letter in bold (for example vector p is written as p) or it can be represented by an arrow placed over a letter (for example vector is written as 
.
Position and displacement vectors:
A position vector describes the position of a point in a coordinate system.
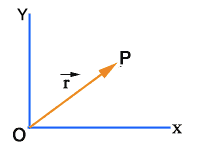
Figure:5.b
If P is the position of an object at time t, then OP is the position vector of the object at that time. It is denoted by 
.
The displacement vector describes the position of a point with reference to a point other than the origin of the coordinate system.
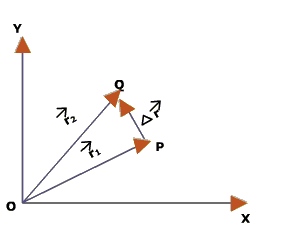
Figure:5.c
An object moves from a point P to point Q. Let 
 is the position vector at a time $t_{1}$ and 
is the position vector at a time $t_{2}$.
is the displacement vector directed from point P to Q, corresponding to the motion of the object from P to Q.
Parallel vectors and antiparallel vectors:
Parallel vectors act along the same direction and they are collinear. The angle between them is $0^{0}$.
Figure:5.d
Antiparallel vectors act in the opposite direction and they are collinear. The angle between them is $180^{0}.$
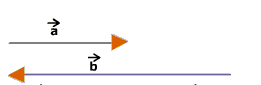
Figure:5.e
Equality of vectors:
Two vectors are said to be equal if they have the same magnitude and direction.
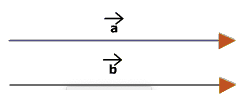
Figure:5.f
Unit vector:
Unit vector has a unit magnitude and points in a particular direction. Any vector 
can be written as the product of unit vector in that direction and magnitude of the given vector.
Unit vector is expressed as 
.
We can write, 
= 
$p$
A unit vector has no dimensions. Unit vectors along the positive X, Y and Z -axes of the coordinate system can be expressed as
such that 
.
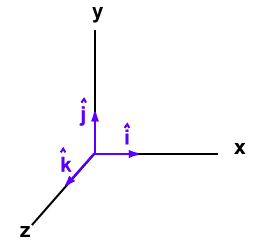
Figure:5.g
