Velocity Vector

A position vector describes the position of a point in a coordinate system.

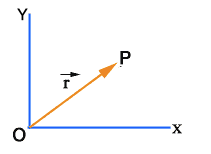
Figure:7.a

If P is the position of an object at time t, then OP is the position vector of the object at that time. It is denoted by .

Displacement vector describes the position of a point with reference to a point other than the origin of the coordinate system.

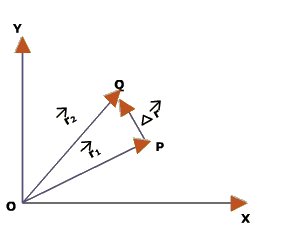
Figure:7.b

An object moves from a point P to point Q. Let is the position vector at time $t_{1}$ and  is the position vector at time $t_{2}$.

is the displacement vector directed from point P to Q, corresponding to the motion of the object from P to Q.

The average velocity of an object is the ratio of the displacement and the corresponding time interval.

Or,

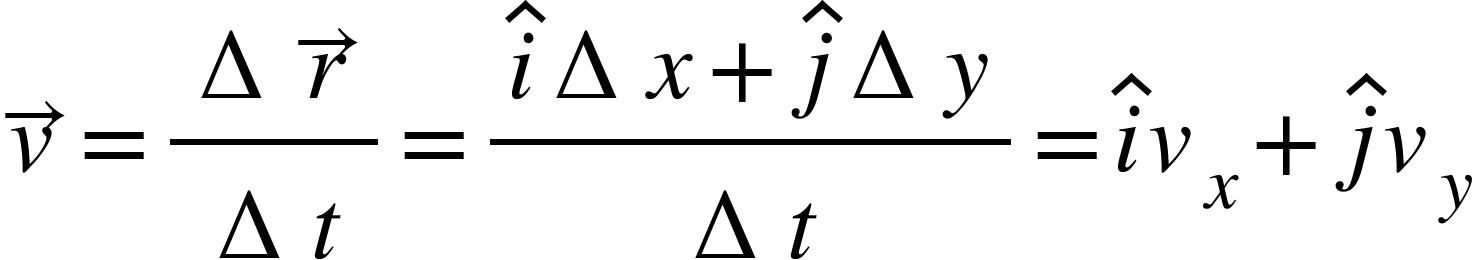
The instantaneous velocity is given by the limiting value of the average velocity as the time interval approaches zero.

The instantaneous velocity vector is always tangential to the path at the point that locates the position of the object.

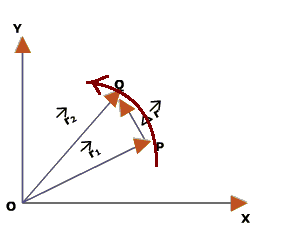
Figure:7.c

Also, we have,

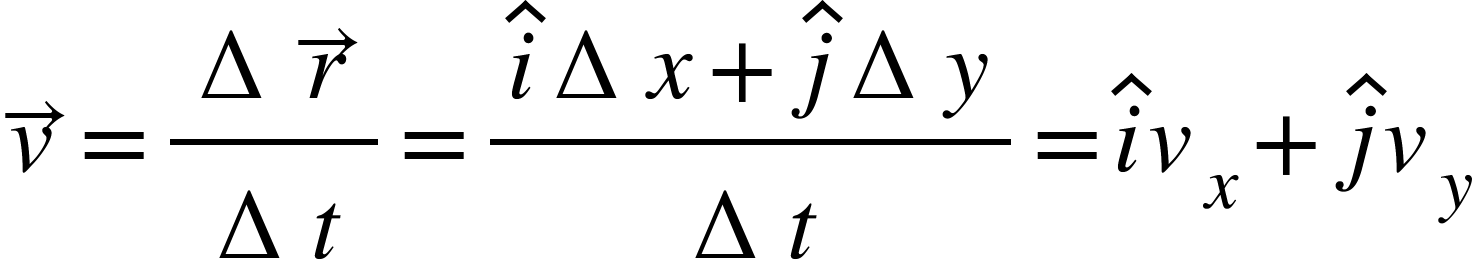
The magnitude of is given by,

$\vert v\vert =\sqrt{v_{x}^{2}+v_{y}^{2}}$

And the direction is given by,

$\theta =\tan ^{-1}\frac{v_{y}}{v_{x}}$

Acceleration:

The average acceleration of an object for a time interval t is the change in velocity divided by the time interval.

Or,

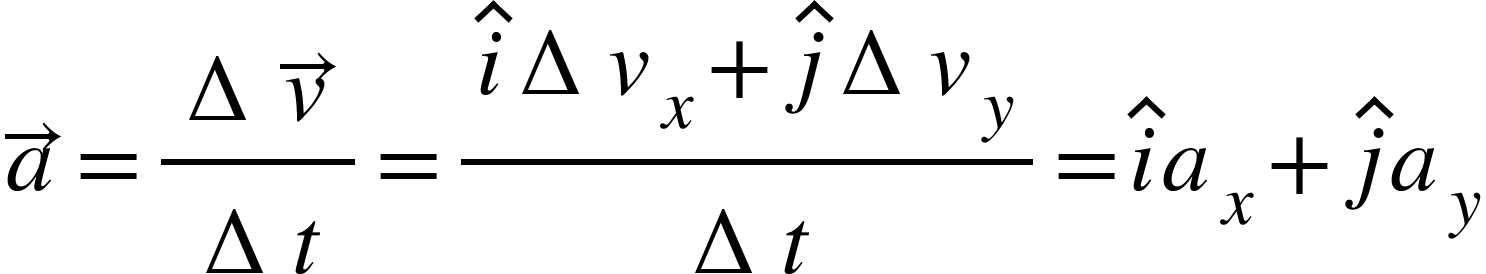
The instantaneous acceleration is given by the limiting value of the average acceleration as the time interval approaches zero. The instantaneous acceleration is shown at point P in the below diagram.

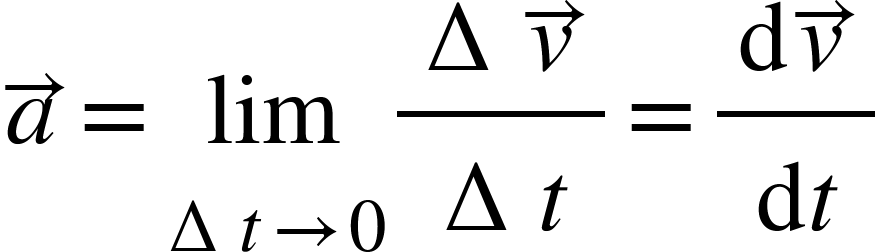
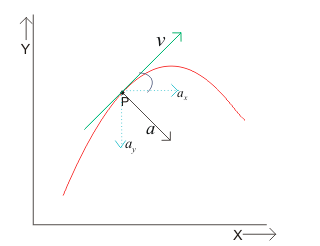
Figure:7.d

As $\Delta t$ decreases, the direction of velocity changes and consequently, the direction of the acceleration changes. When $\Delta t$tends to zero, the average acceleration becomes the instantaneous acceleration and has the direction as shown in figure 7.d.

Instantaneous acceleration does not have the same direction as that of velocity vector.

Velocity and acceleration vectors may have any angle between $0^{0}$ and $180^{0}$between them.

Relative velocity in two dimensions:

Earlier we have studied that if two objects A and B are moving with uniform velocities $V_{A}$and $V_{B}$ along the same direction respectively, then:

relative velocity of A with respect to B is $V_{AB}=V_{A}-V_{B}$ ………….. (1)

And relative velocity of B with respect to A is $V_{BA}=V_{B}-V_{A}$ ………. (2)

Now components of velocity of object A along the X and Y-directions,

……………. (3)

Components of velocity of object B along the X and Y-directions,

…………….. (4)

From equation (1), we get,

Or,

Similarly,

Conceptual question:

1. Show that the relative speed between two objects moving in opposite directions is equal to the sum of their individual speeds.

We have,

As the objects are moving in opposite directions, then $\theta =180^{0}$.

Therefore,

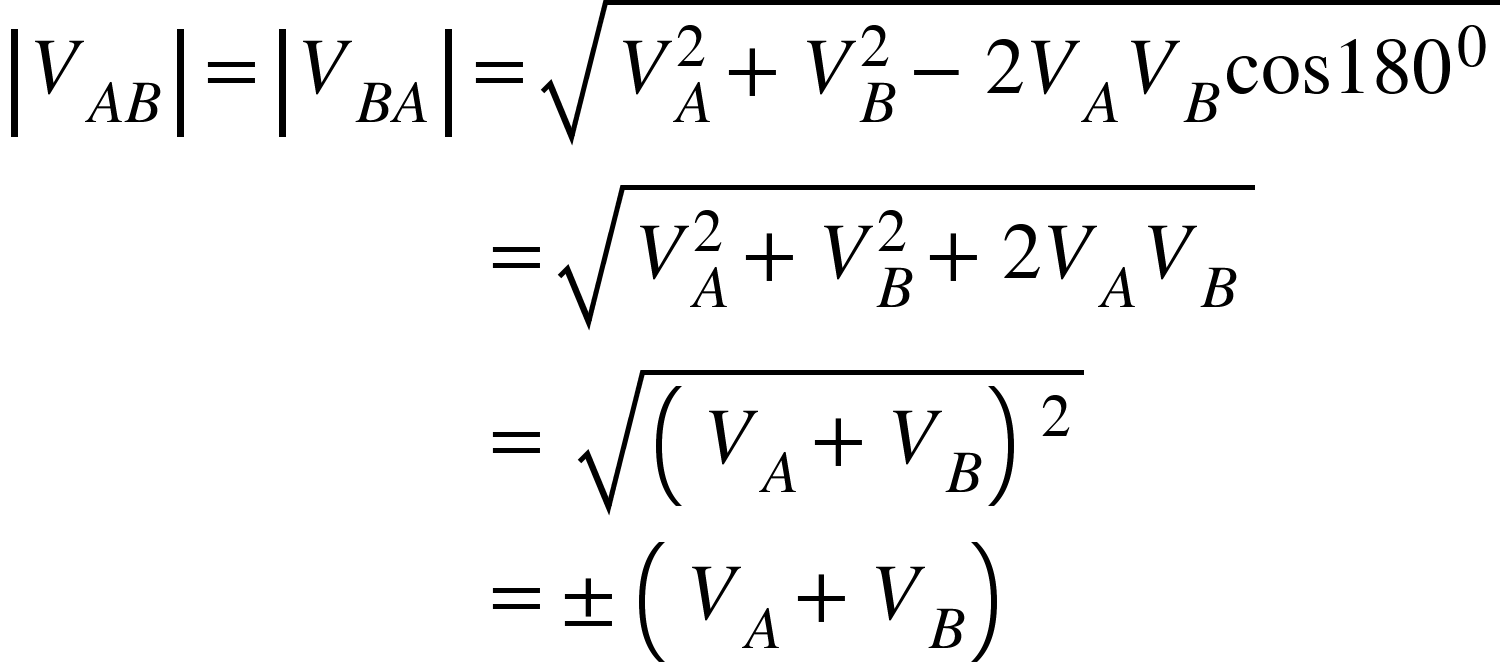
As speed cannot be negative, therefore,

Thus, the relative speed between two objects moving in opposite directions is equal to the sum of their individual speeds.